توضیحات
این مقاله روشی را برای ادغام عددی یک سیستم به هم پیوسته، بر اساس یک ایده از تقریب متعامد توابع، پیشنهاد میکند. در اینجا، توابع پالس بلوک (BPFs) به عنوان مجموعه متعامد انتخاب می شوند. مزیت اصلی استفاده از این تکنیک توانایی آن در تبدیل مسئله کنترل بهینه اصلی به یک مسئله برنامه ریزی ریاضی است که حل آن نسبتاً ساده تر است. تمرکز اصلی این مقاله، بهرهبرداری و توسعه دقیق تکنیک پارامترسازی BPFs برای سنتز یک کنترل بهینه مبتنی بر ناظر غیرمتمرکز برای سیستمهای بهم پیوسته در مقیاس بزرگ است. علاوه بر این، ما یک مدل ریاضی از یک آونگ معکوس دو موازی که توسط یک فنر جفت شده است، با در نظر گرفتن تمام تغییرات ممکن در موقعیت اتصال فنر الاستیک ایجاد می کنیم. با انجام این کار، شبیهسازیهای پیشرفته را با اعمال روش کنترل بهینه جدید برای سیستم به هم پیوسته مورد مطالعه انجام دادیم. نتایج ما اعتبار و اثربخشی رویکرد کنترل بهینه مبتنی بر ناظر غیرمتمرکز توسعهیافته را نشان میدهد.
در دهههای اخیر، بخش مهمی از فعالیتهای تحقیقاتی در خودکار بر مسئله کنترل بهینه با مشارکتهای متعدد در تئوری متمرکز شده است. فرمول بندی مسئله کنترل بهینه اساسی یک فرآیند را می توان به صورت زیر خلاصه کرد: از آنجایی که یک فرآیند با مدل آن ارائه و تعریف می شود، باید از بین دستورات قابل قبول، دستوری را انتخاب کنیم که همزمان اجازه می دهد شرایط اولیه و نهایی داده شده را تأیید کند. ، ارضای محدودیت های تحمیلی مختلف بر روی حرکت سیستم و بهینه سازی (به حداقل رساندن یا حداکثر کردن) یک شاخص عملکرد مشخص. در زمینههای مختلفی مانند سیستمهای خودرو، سیستمهای انرژی، هوافضا، رباتیک، تولید برق، سیستمهای توزیع و غیره استفاده شده است. آنیل، 2009؛ فلمینگ و ریشل، 2012؛ کرک، 2012). روش های عددی به دو دسته عمده تقسیم می شوند: روش های غیر مستقیم و مستقیم (فون و بولیرش، 1992). در روش غیرمستقیم، دو روش رایج حل مسئله کنترل بهینه عبارتند از اصل حداکثر پونتریاگین و معادله همیلتون-جاکوبی-بلمن (باردی و کاپوزو-دولستا، 2008؛ هارتل و همکاران، 1995). در روش مستقیم، مسئله کنترل بهینه با استفاده از تکنیکهای گسستهسازی یا پارامترسازی به یک مسئله برنامهریزی غیرخطی رونویسی میشود (Kraft، 1985؛ Sie-Long، 2013). دسته دوم حل مسئله توجه بسیاری از محققین را به خود جلب کرده است. در حقیقت، بسیاری از روشهای مستقیم در ادبیات توسعه یافتهاند، مانند روش همآهنگی هرمیت سیمپسون (Becerra, 2010)، چند جملهای چبیشف (Jaddu, 1998)، شبه خطیسازی (نیری و کامیاد، 2014) و روش توابع پالس بلوکی (عبداللهی و بابلیان، 1395؛ خواجه نصیری، 1393؛ موهن و کار، 1391؛ یونس پور و غفارزاده، 1394؛ زرینی و ترکمن، 1393) که موضوع مطالعه ما است.
هدف
کنترل بهینه پاندول معکوس دوگانه موازی با استفاده از روش BPFs
در این گزارش ۱) معادلهی دینامیکی سیستم بیان میشود، ۲) معادلهی سیستم و مشاهدهگر با استفاده از قانون کنترل فیدبک بهینه به دست میآید. ۳) با اعمال BPFs بر سیستم، معادلهی دیفرانسیل سیستم به معادلهی جبری تبدیل میشود. ۴) نتایج شبیهسازی معادلهی سیستم دو درجه آزادی پاندول معکوس دوگانه موازی با استفاده از روش BPFs نشان داده میشود.
۱) معادله ی دینامیکی سیستم
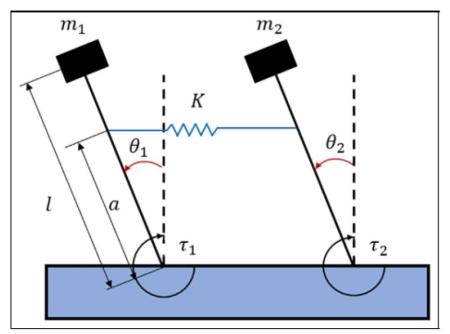
با توجه به درجات آزادی سیستم ، معادلهی دینامیکی به صورت زیر به دست می آید.
۴) شبیه سازی
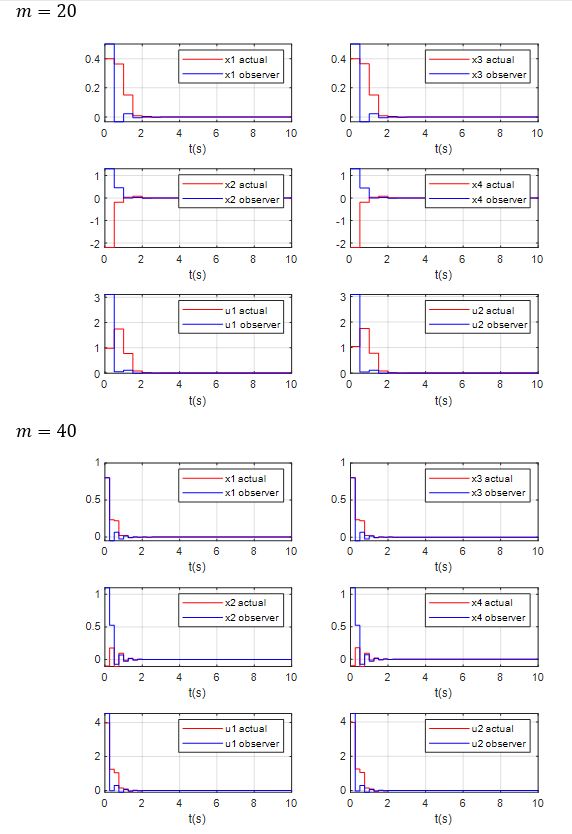
در این بخش با حل معادلات جبری سیستم با توجه به پهنای باندهای متفاوت رفتار سیستم بررسی میشود. با توجه به نتایج، با کاهش پهنای باند که نشان از تخمین حالتها در بازهی زمانی کوچکتری دارد، بهبود عملکرد سیستم در همگرایی مقادیر حالتهای سیستم به سمت نقطهی تعادل را نشان میدهد.
در ادامه نتایج سیستم به ازای مقادیر مختلف m و h نشان داده شده است.
- فایلهای پروژه به صورت کامل پس از خرید فایل بلافاصله در اختیار شما قرار خواهد گرفت.











نقد و بررسیها
هنوز بررسیای ثبت نشده است.