توضیحات
ﺑﺨﺶ اول) ﭘﺎﯾﺪاري ﺳﯿﺴﺘﻢ ﻫﺎي دﯾﻨﺎﻣﯿﮑﯽ ﺧﻄﯽ
ﭘﺎﯾﺪاري / ﻧﺎﭘﺎﯾﺪاري
در ﯾﮏ ﺳﯿﺴﺘﻢ دﯾﻨﺎﻣﯿﮑﯽ ﺧﻄﯽ ﺗﻐﯿﯿﺮﻧﺎﭘﺬﯾﺮ ﺑﺎ زﻣﺎن، زﻣﺎﻧﯽ ﺳﯿﺴﺘﻢ ﭘﺎﯾﺪار ﺧﻮاﻫﺪ ﺑﻮد ﮐﻪ ﻗﻄﺐﻫﺎي ﺳﯿﺴﺘﻢ در ﺻﻔﺤﻪ ﻣﺨﺘﻠﻂ s در ﺳﻤﺖ ﭼﭗ ﻣﺤﻮر 𝑗𝜔 ﻗﺮار داﺷﺘﻪ ﺑﺎﺷﻨﺪ. در ﺻﻮرﺗﯿﮑﻪ ﻗﻄﺐﻫﺎي ﺳﯿﺴﺘﻢ در ﺳﻤﺖ راﺳﺖ ﻣﺤﻮر 𝑗𝜔 ﻗﺮار داﺷﺘﻪ ﺑﺎﺷﻨﺪ ﺳﯿﺴﺘﻢ ﻧﺎﭘﺎﯾﺪار ﺧﻮاﻫﺪ ﺑﻮد. ﻗﺮار ﮔﺮﻓﺘﻦ ﻗﻄﺐﻫﺎي ﺳﯿﺴﺘﻢ روي ﻣﺤﻮر 𝑗𝜔 ﺣﺎﻟﺖ وﯾﮋه ﭘﺎﯾﺪار ﻣﺮزي (ﺣﺎﺷﯿﻪاي) را اﯾﺠﺎد ﻣﯽﮐﻨﺪ؛ در اﯾﻦ ﺷﺮاﯾﻂ ﺳﯿﺴﺘﻢ ﺑﻪ ازاي ﺑﺮﺧﯽ وروديﻫﺎي ﮐﺮاﻧﺪار ﺧﺮوﺟﯽ ﮐﺮاﻧﺪار و ﺑﻪ ازاي ﺑﺮﺧﯽ وروديﻫﺎي ﮐﺮاﻧﺪار ﭘﺎﺳﺦ ﺑﯽﮐﺮان ﺧﻮاﻫﺪ داﺷﺖ (ﭘﺎﯾﺪاري 𝐵𝐼𝐵𝑂 را ﻧﻘﺾ ﻣﯽ ﮐﻨﺪ). ﻧﻤﻮﻧﻪ ﭼﻨﯿﻦ ﺳﯿﺴﺘﻤﯽ ﯾﮏ اﻧﺘﮕﺮالﮔﯿﺮ ﺳﺎده اﺳﺖ ﮐﻪ در آن ﻗﻄﺐ ﺳﯿﺴﺘﻢ روي 0 =𝑠 ﻗﺮار دارد. اﯾﻦ ﺳﯿﺴﺘﻢ ﺑﻪ ورودي ﮐﺮاندار ﭘﻠﻪ واﺣﺪ ﺧﺮوﺟﯽ ﺑﯽﮐﺮان ﺷﯿﺐ واﺣﺪ و ﺑﻪ ازاي ورودي ﺿﺮﺑﻪ واﺣﺪ ﺧﺮوﺟﯽ ﭘﻠﻪ واﺣﺪ ﺧﻮاﻫﺪ داﺷﺖ.
ﻣﻮﻗﻌﯿﺖ ﻧﺴﺒﯽ ﻗﻄﺐ(ﻫﺎي) ﺳﯿﺴﺘﻢ را ﻧﺴﺒﺖ ﺑﻪ ﻣﺤﻮر 𝑗𝜔 ﺑﺪﺳﺖ آورده ایم.
- ﺧﺮوﺟﯽ ﺳﯿﺴﺘﻢ را ﺑﻪ ازاي ورودي ﭘﻠﻪ واﺣﺪ ﺗﺮﺳﯿﻢکرده ایم.
- ﺧﺮوﺟﯽ ﺳﯿﺴﺘﻢ را ﺑﻪ ازاي ورودي 𝑠𝑖𝑛(4𝑡) ترسیم کرده ایم. برای سیستم c ﭘﺎﺳﺦ ﺳﯿﺴﺘﻢ ﺑﻪ ورودي 2𝑠𝑖𝑛(5𝑡) را ﻧﯿﺰ ﺗﺮﺳﯿﻢ ﮐﺮده وﺗﺤﻠﯿﻞ ﻻزم را اراﺋﻪ کرﺪه ایم.
- بررسی کرده ایم که ﺳﯿﺴﺘﻢ ﮐﺪامﯾﮏ از ﺧﻮاص ﭘﺎﯾﺪاري(ﭘﺎﯾﺪار/ﭘﺎﯾﺪار ﺣﺎﺷﯿﻪاي/ﻧﺎﭘﺎﯾﺪار)را داراﺳﺖ؟
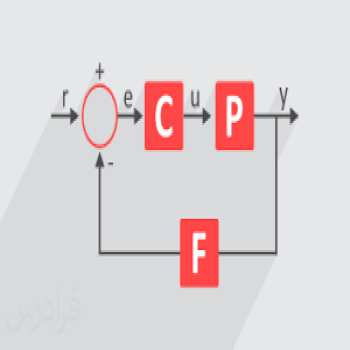
ﺑﺨﺶ دوم( ﻣﻘﺎﯾﺴﻪ ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز و ﺣﻠﻘﻪ ﺑﺴﺘﻪ
1-2- ﺑﺮرﺳﯽ ﺳﺮﻋﺖ ﺳﯿﺴﺘﻢ
ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز زﯾﺮ را در ﻧﻈﺮ ﺑﮕﯿﺮﯾﺪ:
ﺑﺎ در ﻧﻈﺮ ﮔﺮﻓﺘﻦ 𝜏 = 3 𝑠𝑒𝑐 در ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز، ﭘﺎﺳﺦ ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز ﺑﻪ ورودي ﭘﻠﻪ واﺣﺪ را ﺑﺪﺳﺖ آورده و ﺗﺮﺳﯿﻢ ﮐردیم.
ﺑﺎ در ﻧﻈﺮ ﮔﺮﻓﺘﻦ 𝜏 = 3 𝑠𝑒𝑐 در ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز، ﺣﻠﻘﻪ ﻓﯿﺪﺑﮏ ﺳﯿﺴﺘﻢ را ﺑﺎ ﻓﯿﺪﺑﮏ واﺣﺪ ﻣﻨﻔﯽ بسﺘﻪ و ﺧﺮوﺟﯽ ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺴﺘﻪ را ﺗﺮﺳﯿﻢ ﮐرﺪیم.
ﭘﺎﺳﺦ ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز و ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺴﺘﻪ را از ﻧﻈﺮ ﺳﺮﻋﺖ رﺳﯿﺪن ﺑﻪ ﺣﺎﻟﺖ ﻣﺎﻧﺪﮔﺎر ﺑﺮرﺳﯽکرده ایم.
2-2- ﺑﺮرﺳﯽ ﻗﻮام ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز و ﺣﻠﻘﻪ ﺑﺴﺘﻪ در اﺛﺮ ﺗﻐﯿﯿﺮ ﭘﺎراﻣﺘﺮ
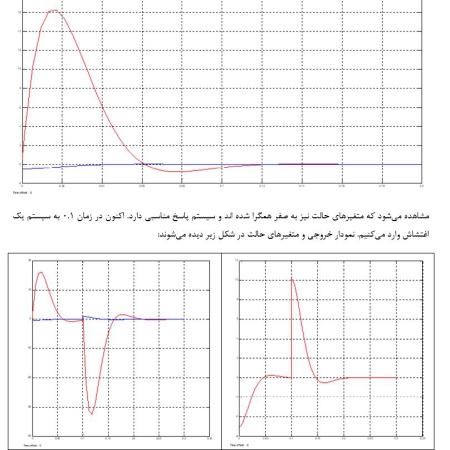
ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺎز ﻣﻄﺮح در اﺑﺘﺪاي ﺑﺨﺶ ﺳﻮم را در ﻧﻈﺮ ﺑﮕﯿﺮﯾﺪ، ﭼﻨﺎﻧﭽﻪ ﻣﻘﺪار ﺣﻘﯿﻘﯽ 𝜏 ﺑﺮاﺑﺮ ﺑﺎ 4 ﺛﺎﻧﯿﻪ ﺑﺎﺷﺪ ﭘﺎﺳﺦ ﺳﯿﺴﺘﻢ واﻗﻌﯽ و ﺳﯿﺴﺘﻢ ﻣﺪل ﺷﺪه ﺑﺎ 𝜏 = 3 𝑠𝑒𝑐 را ﺗﺮﺳﯿﻢ ﮐﺮده و ﺳﺮﻋﺖ رﺳﯿﺪن اﯾﻦ ﭘﺎﺳﺦ ﻫﺎ ﺑﻪ ﺣﺎﻟﺖ ﻣﺎﻧﺪﮔﺎر را ﻣﻘﺎﯾﺴﻪ ﮐرﺪه ایم. اﮐﻨﻮن ﺳﯿﺴﺘﻢ را ﺑﺎ ﺣﻠﻘﻪ ﻓﯿﺪﺑﮏ واﺣﺪ ﻣﻨﻔﯽ در ﻧﻈﺮ ﺑﮕﯿﺮﯾﺪ. ﭘﺎﺳﺦ ﺳﯿﺴﺘﻢ ﺣﻠﻘﻪ ﺑﺴﺘﻪ ﺑﻪ ازاي ﻫﺮ دو ﺣﺎﻟﺖ 𝜏 = 3 sec , 𝜏 = 4 𝑠𝑒𝑐 را رﺳﻢ ﮐﺮده و اﺧﺘﻼف در ﺳﺮﻋﺖ رﺳﯿﺪن ﺑﻪ ﺣﺎﻟﺖ ﻣﺎﻧﺪﮔﺎر در اﯾﻦ دو ﺣﺎﻟﺖ را ﺑﺎ ﯾﮑﺪﯾﮕﺮ ﻣﻘﺎﯾﺴﻪ ﮐرﺪه ایم. بررسی کرده ایم که اﺛﺮ ﺗﻐﯿﯿﺮ در ﭘﺎراﻣﺘﺮ 𝜏 در ﮐﺪام ﺣﺎﻟﺖ (ﺣﻠﻘﻪ ﺑﺎز ﯾﺎ ﺣﻠﻘﻪ ﺑﺴﺘﻪ)ﺑﯿﺸﺘﺮ ﺧﻮدﻧﻤﺎﯾﯽ ﻣﯽ ﮐﻨﺪ؟ ﭼﺮا؟
بخشی از گزارش کار:
بخش اول: پایداری سیستمهای دینامیکی خطی
پایداری / ناپایداری
در یک سیستم دینامیکی خطی تغییرناپذیر با زمان، زمانی سیستم پایدار خواهد بود که قطبهای سیستم در صفحه مختلط s در سمت چپ محور قرار داشته باشند. در صورتی که قطبهای سیستم در سمت راست محور قرار داشته باشند سیستم ناپایدار خواهد بود. قرار گرفتن قطبهای سیستم روی محور حالت ویژه پایدار مرزی (حاشیهای) را ایجاد میکند؛ در این شرایط سیستم به ازای برخی ورودیهای کراندار خروجی کراندار و به ازای برخی ورودیهای کراندار پاسخ بیکران خواهد داشت (پایداری BIBO را نقض میکند). نمونه چنین سیستمی یک انتگرالگیر ساده است که در آن قطب سیستم روی قرار دارد. این سیستم به ورودی کراندار پله واحد خروجی بیکران شیب واحد و به ازای ورودی ضربه واحد خروجی پله واحد خواهد داشت.
- موقعیت نسبی قطب(های) سیستم را نسبت به محور بدست آورید.
تابع تبدیل هر سیستم را با دستور tf تعریف و صفر و قطبهای آن ها را با دستور pzmap یا pzplot رسم میکنیم.
- پروژه شبیه سازی سیستم های خطی حلقه باز و بسته با متلب توسط کارشناسان گروه ۱.۲.۳ پروژه پیاده سازی گردیده.
- فایلهای پروژه به صورت کامل پس از خرید فایل بلافاصله در اختیار شما قرار خواهد گرفت.
-
سفارش پروژه متلب
درصورتیکه این پروژه دقیقا مطابق خواسته شما نمی باشد، با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.





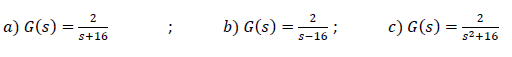
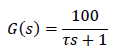










نقد و بررسیها
هنوز بررسیای ثبت نشده است.