توضیحات
پروژه بهینه سازی تخصیص و چیدمان تسهیلات با گمز و متلب
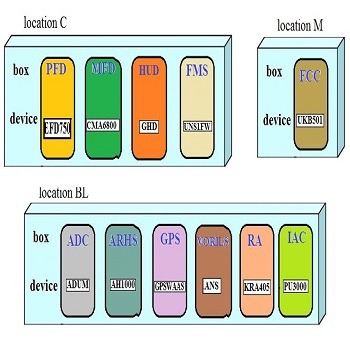
هدف تخصیص بهترین box به نام های زیر از دیتابیس به محل نصب خود با ارضا محدودیت ها.
تعدادی جعبه به نام های ADC، AHRS، VORILS، RA، PFD، MFD، HUD، IAC، FCC، FMS و GPS
هر جعبه با یک وزن، توان مصرفی، قابلیت اطمینان، حجم و توان عملیاتی و شرکت سازنده در دیتابیس ثبت شده اند. برای هر جعبه حداقل 3 جعبه از شرکت مختلف با مشخصات متفاوت موجود است.
تخصیص جعبه از دیتابیس (به نام هر باکس حداقل 3 باکس با مشخصات مختلف وجود دارد)
تخصیص هر جعبه به یک محل نصب مشخص (4 محل نصب با محدودیت های وزن و حجم مشخص شده اند)
محدودیت ها در محل نصب:
محدودیت ها در محل نصب شامل حداکثر وزن و حجم قابل نصب در مکان
|
Volume |
Mass |
Location |
|
3100 |
50 |
C |
|
2500 |
40 |
BL |
|
2500 |
40 |
BR |
|
1000 |
30 |
M |
محدوئیت در نحوه نصب:
جعبه های HUD، PFD، MFD و FMS تنها می توانند در محل نصب C نصب شوند.
جعبه های HUD، PFD، MFD در کنار هم و جدا از FMS نصب می شوند.
جعبه های ADC، AHRS و GPS درتنها محل BL نصب میتوانند نصب شوند. و در کنار هم.
جعبه IAC تنها در محل BL نصب می تواند شود و جدا از جعبه های ADC، AHRS و GPS.
جعبه FCC تنها می تواند در محل نصب M نصب شود.
اهداف:
- کمینه کردن وزن چیدمان نهایی جعبه ها در محل نصب (یعنی از دیتابیس جعبه ای نهایتا به جعبه با نام معین خود اختصاص یابد که منجر به کمینه شدن جمع وزن جعبه های انتخابی شود)
- کمینه کردن وزن چیدمان و بیشبنه کردن قابلیت اطمینان
متغیر های تصمیم:
متغیر باینری برای تخصیص جعبه از دیتابیس
متغیر باینری برای تخصیص جعبه به مکان نصب
روش حل:
روش دقیق شاخه و کران
روش های هیورستیک و یا متاهیورستیک
Definition of parameters:
L: installation location
I: installation resource
Decision variables:
: Binary variable to assign avionics box (b) to device (d)
: Binary variable to assign device (d) to location (l)
مدل سازی مسئله پیشنهادی

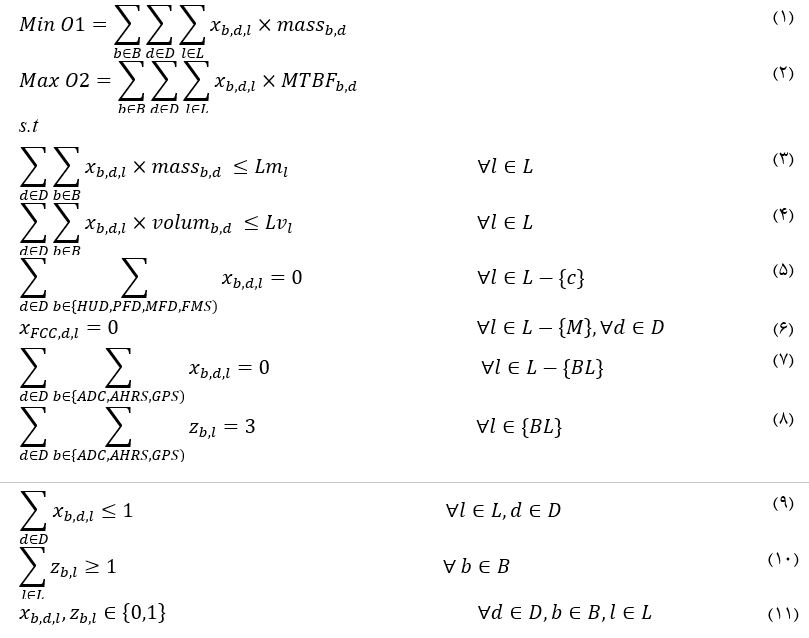
معادلات 1 و 2 توابع هدف مدل پیشنهادی می باشند. معادله (1) وزن چیدمان را حداقل سازی می کند. درجه ی اطمینان معمولا برای بیان کارکرد صحیح یک قطعه یا به طور کلی مجموعه ای از عوامل در طی مدت زمان و دوره ی زمانی مشخص به کار می رود. اما توجه به این نکته ضروری است که اگر قطعه ای خراب شد، بدین معنا نیست که لزوما غیر قابل اعتماد است. بنابراین قابلیت اطمینان هر سیستمی تابعی از میزان فاصله بین هر دو خرابی سیستم می باشد، در مدل پیشنهادی حاضر برای بیشینه سازی قابلیت اطمینان به حداکثر سازی زمان بین هر دو خرابی پرداخته شده، که در معادله (2) بیان شده است. محدویت های (3) و (4) هریک بیان می دارند که وزن و حجم جعبه ها از ظرفیت هر مکان فراتر نرود. محدودیت (5) تضمین می کند که جعبه های HUD، PFD، MFD و FMS تنها می توانند در محل نصب C نصب شوند. محدودیت (6) بیان می کند که جعبه FCC تنها می تواند در محل نصب M نصب شود. محدودیت های (7) و (8) تضمین می کند که جعبه های ADC، AHRS و GPS تنها در محل BL و در کنار هم می توانند نصب شوند. محدودیت (9) تضمین می کند که به هر جعبه تنها یک دستگاه اختصاص پیدا می کند. نامعادله (10) نشان می دهد که تمامی جعبه ها حتما باید تخصیص داده شوند. محدودیت 11 نیز تعریف کننده ی متغیرهای تصمیم مسئله می باشد. انجام پروژه صنایع
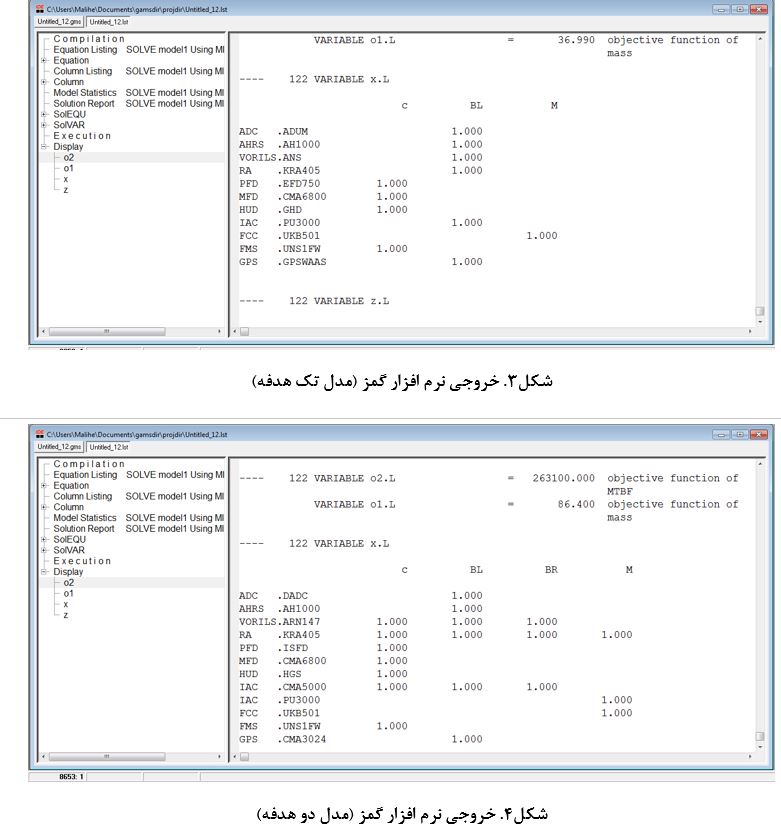
نتایج عدی
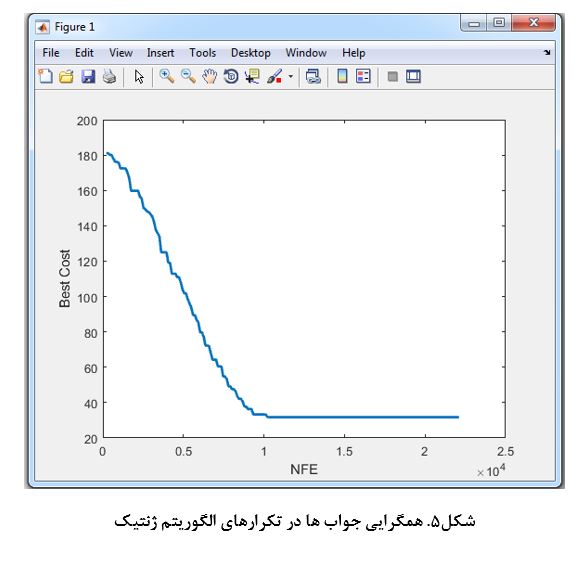
نتایج محاسباتی در این بخش به منظور بررسی و ارزیابی عملکرد مدل پیشنهادی دو هدفه ارائه شده است. داده های آزمایشی مسئله مورد بررسی با استفاده از دیتابیس موجود در فایل اکسل، آورده شده است. حل دقیق مدل ریاضی برنامه ریزی عدد صحیح غیرخطی پیشنهادی در نرمافزار گمز نسخهی 25.1.2 با استفاده از حلکننده BONMIN که از روش شاخه و کران برای حل استفاده می کند، انجام شده است. الگوریتم NSGAII کلاسیک نیز توسط نرم افزار MATLAB R2017b کد شده و بر روی کامپیوتر با پردازشگر و حافظه اجرا شده است. برای چند هدفه بودن مسئله نیز از روش حل معیار جامع (LP-متریک[1]) استفاده شده است. روش معیار جامع از روشهای تصمیم گیری چند معیاره (MCDM) است که به حل مدل های تصمیم گیری چند هدفه (MODM) می پردازد. تکنیک های برنامه ریزی آرمانی و معیار جامع، از متدولوژی های مطرح در تصمیم گیری با معیارهای چندگانه می باشند. این رویکردها دارای ریشه مشترک هستند و از یک نقطه هدف قطعی در فضای معیار به منظور مدل سازی ترجیحات تصمیم گیرنده استفاده می کنند. در تکنیک معیار جامع این نقطه هدف، برداری از سطوح مرجع است (اوگریشاک[2]، 2001). در این روش مجموع توان انحرافات نسبی اهداف از مقدار بهینه شان حداقل می شود. بدین صورت که برای یک مسئله با n تابع هدف باید مقدار بهینه هر تابع هدف را (از اولین تا nمین) مستقل از بقیه n-1 تابع هدف دیگر و با در نظر گیری تمامی محدودیت های مساله حساب شود. از آنجایی که هرچه توابع هدف به مقادیر بهینه شان نزدیک تر باشد، مطلوب تر است بنابراین به دنبال تابع هدفی هستیم که با استفاده از آن همه توابع به مقدار بهینه شان نزدیک شوند بدین منظور باید مجموع انحراف های نسبی اهداف از مقادیر بهینه شان حداقل شود. انجام پروژه متلب
پروژه بهینه سازی تخصیص و چیدمان تسهیلات با گمز و متلب توسط کارشناسان گروه ۱.۲.۳ پروژه پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
- فایلهای پروژه به صورت کامل پس از خرید فایل بلافاصله در اختیار شما قرار خواهد گرفت.
سفارش پروژه مشابه
درصورتیکه این پروژه دقیقا مطابق خواسته شما نمی باشد، با کلیک بر روی کلید زیر پروژه دلخواه خود را سفارش دهید.












نقد و بررسیها
هنوز بررسیای ثبت نشده است.