توضیحات
پروژه مدلسازی سیستم قطار با متلب:
خلاصه محتویات فایل پروژه:
- پروژه به صورت کامل در سیمولینک و متلب شبیه سازی و پیاده سازی شده است
- مراحل انجام کار به صورت گام به گام در فایل راهنما شرح داده شده است
- لینک دانلود فایلهای مربوط به پروژه پس از خرید فایل بلافاصله برای شما ایمیل خواهد شد.
- فایلهای کامل پروژه قابل اجرا در نرم افزار متلب
- فایل راهنما
خلاصه پروژه:
مقدمه:
ما می خواهیم یک قطار اسباب بازی که شامل یک لوکوموتیو و یک واگن است را توسط نرم افزار متلب بررسی کنیم. فرض میکنیم که قطار فقط در یک جهت سفر می کند .ما می خواهیم کنترل را بر روی قطار اعمال کنیم چونکه قطار آغاز حرکت (لحظه راه اندازی) و توقف آرام و روانی دارد و به علاوه یک سرعت حرکت ثابت.
هدف از این پروژه صرفا مدلسازی و طراحی یک کنترلر برای سیستم قطار به وسیله معادلات فضای حالت در نرم افزار متلب است.
در این پروژه ابتدا معادله حالت حرکت و متغیرهای حالت و روابط خروجی را به دست می آوریم سپس تابع انتقال سیستم را و پس از آن فرم فضای حالت سیستم را به دست آورده و به مدلسازی آن در متلب می پردازیم.
1- طرح مسئله
شکل1-1 یک قطار شامل یک لوکوموتیو و یک واگن را نشان می دهد. جرم لوکوموتیو و واگن را به ترتیب با M1 و M2 نمایش می دهیم. این دو با یک فنردر کنار هم نگه داشته شده اند و ضریب سختی فنر را با K , نیروی به کار برده شده توسط لوکوموتیو با F و اصطکاک بین چرخ ها و ریل را با حروف یونانی μ نشان می دهیم.
یک قطار شامل لوکوموتیو و یک واگن
نحوه اجرای کار:
شبیه سازی این برنامه با کدنویسی و در قسمت editor متلب نوشته شده است و مراحل شبیه سازی به صورت زیر میباشد.
در قسمت اول که با نام %% 1: Data مشخص شده است داده های مساله و ماتریس های حالت فراخوانی شده اند.
در قسمت دوم که با نام %% 2: Create System مشخص گردیده سیستم به دو صورت فضای حالت و قطب و صفر تعریف شده است. ابتدا با دستور ss سیستم با نام Sys بصورت فضای حالت تعریف شده است. در خط بعدی برنامه سیستم را از فضای حالت به حوزه ی لاپلاس برده و در خط بعد آن تابع تبدیل سیستم را که با نام G مشخص شده است را ایجاد میکنیم.
سپس تابع تبدیل حلقه بسته را تشکیل داده و قطب های حلقه باز و حلقه بسته را تشکیل میدهیم.
در قسمت سوم با نام %% 3: Calcute Eigenvalues مقادیر ویژه سیستم را بدست میآوریم. و در قسمت چهارم کنترل پذیری و رویت پذیری را بررسی میکنیم که این سیستم کنترل پذیر ولی رویت ناپذیر است. و با اجرای برنامه این امر در محیط متلب نشان داده میشود.
در قسمت پنجم فیدبک حالت را تعریف میکنیم. در اینجا به دلخواه قطب های حلقه بسته را
[-4+1.58*1i -4-1.58*1i -4 -5]در نظر میگیریم. این انتخاب دلخواه بوده و هر مقدار دیگری میتواند باشد.
سپس سیستم حلقه بسته را تشکیل داده و تابع تبدیل حلقه بسته را بدست می اوریم.
در قسمت ششم دیاگرام بود و نایکوییست رسم شده است. و در قسمت هفتم نیز مکان هندسی ریشه ها رسم شده است.
در نهایت در قسمت هشتم پاسخ پله به ازای شرایط اولیه ی x0=[10 0 0 0] برای سیستم حلقه بسته و حلقه باز رسم میکنیم.
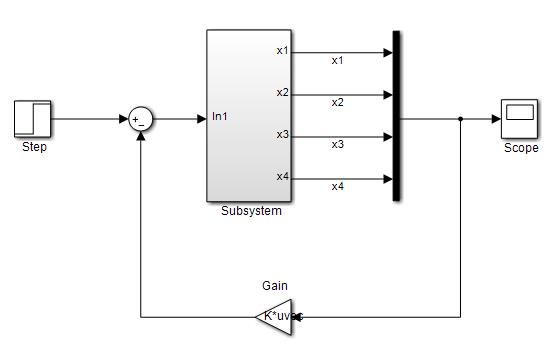
تصویر نتایج شبیه سازی:
نکات قابل ذکر:
- پروژه مدلسازی سیستم قطار با متلب توسط کارشناسان گروه ۱.۲.۳ پروژه پیاده سازی گردیده و به تعداد محدودی قابل فروش می باشد.
- فایل های پروژه به صورت کامل به همراه فایل راهنما پس از خرید فایل در اختیار شما قرار خواهد گرفت، و شما به راحتی قادر به استفاده از پروژه خواهید بود.










نقد و بررسیها
هنوز بررسیای ثبت نشده است.