توضیحات
شبیه سازی آموزشی تنظیم خودکار کنترلر PID بر اساس پاسخ مرحله فرآیند و معیار بهینه میرایی با متلب
چکیده مقاله (ترجمه ماشینی)
این مقاله یک روش جدید برای تنظیم کنترلر PID مناسب برای فرآیندهای دورهای مرتبه بالاتر و با هدف برنامههای تنظیم خودکار مبتنی بر پاسخ مرحله ارائه میکند. تنظیم کنترلر PID بر اساس شناسایی مدل فرآیند به اصطلاح تاخیر مرتبه n (PTn) و استفاده از معیار بهینه میرایی است، بنابراین قوانین جبری ساده را برای تنظیم سرعت پاسخ حلقه بسته و میرایی تسهیل میکند. شناسایی مدل PTn بر اساس پاسخ مرحله فرآیند است، که در آن پارامترهای مدل PTn به روشی جدید از پاسخ مرحله فرآیند معادل زمان مرده و ثابت زمان تاخیر ارزیابی میشوند. اثربخشی روش تخمین پارامتر مدل PTn پیشنهادی و تنظیم خودکار کنترلکننده PID مبتنی بر میرایی بهینه مربوطه با استفاده از شبیهسازیهای کامپیوتری گسترده تأیید شده است.
معرفی
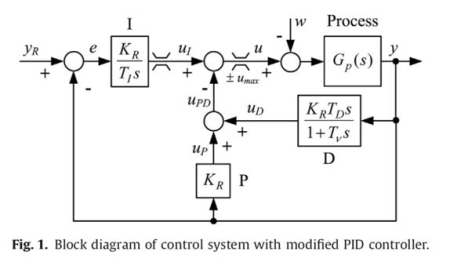
کنترل کننده PI برای جبران اختلال بار و اثر فیلتر در طی شناسایی مدل فرآیند [19]. برای بررسی نسبتاً جامع روشهای تنظیم خودکار دامنه فرکانس بازخورد رله، خواننده نیز به [20] مراجعه میکند. رویکردهای پاسخ زمانی مبتنی بر (i) یکپارچه سازی چندگانه خروجی فرآیند و تحلیل رگرسیون به منظور یافتن پارامترهای یک مدل فرآیند مرتبه دوم به اضافه زمان مرده (SOPDT) [21]، (ii) ادغام چند مرحله ای پاسخ فرآیند برای یافتن یک مدل فرآیند خطی کلی [22-24] همراه با استفاده از معیار بهینه بزرگی به منظور دستیابی به پاسخ حلقه بسته با میرایی خوب، و (iii) شناسایی مرحله-پاسخ مدل FOPDT همراه با رویکرد تنظیم IMC [25،26]، یا یک طراحی کنترل کننده حلقه شکل قوی (به اصطلاح روش AMIGO) [26،27]. رویکردهای ترکیبی که در آن از شناسایی مدل فرآیند حوزه زمان و حوزه فرکانس استفاده میشود، مانند شناسایی مرحله آزمایش رله ترکیبی از یک مدل فرآیند FOPDT [28]، یا تخمین پارامترهای فرآیند برانگیختگی مبتنی بر سیگنال و فرآیند SOPDT و تنظیم کنترلکننده. بر اساس شرطی شدن قطب صفر (لغو) [29]. با این حال، در بیشتر موارد بالا، تنظیم کنترلکننده PID بر اساس تقریب مدل فرآیند نسبتاً ساده FOPDT (یا SOPDT) با تقریبهای زمان مرده Taylor یا Padé مرتبه اول است که برای طراحی کنترلکننده PID استفاده میشود، که ممکن است چنین نباشد. در حضور پویایی فرآیندهای مرتبه بالاتر بارزتر است. به منظور به تصویر کشیدن دینامیک مرتبه بالاتر، در حالی که به طور همزمان دارای یک فرمول نسبتا ساده مدل فرآیند بدون زمان مرده است، یک مدل فرآیند تاخیر مرتبه n (به اصطلاح مدل PTn) می تواند به راحتی استفاده شود، که در آن روابط تحلیلی بین PTn پارامترهای مدل و مدل FOPDT معمولاً از طریق معادل سازی مماس خمش پاسخ گامی مدل فرآیند (به اصطلاح روش Strejc) داده می شود [30،31]. با استفاده از مدل فرآیند PTn به عنوان مبنای طراحی سیستم کنترل در [32]، عبارات تحلیلی ساده ای برای پارامترهای کنترل کننده PID بر اساس معیار بهینه بزرگی به دست آمده است (به عنوان مثال [33] و مراجع در آن مراجعه کنید). پارامترهای مدل PTn در [32] با استفاده از روش به اصطلاح گشتاور (به عنوان مثال [30]) شناسایی شده اند، که از طریق ادغام های چندگانه با وزن زمانی خروجی فرآیند پیاده سازی شده است، بنابراین از تخمین مماس خمش پاسخ مرحله فرآیند اجتناب می شود. شیب (و مسائل مربوط به نویز اندازه گیری). از آنجایی که مزیت اصلی معیار بهینه بزرگی این است که می تواند پاسخ سیستم حلقه بسته با میرایی خوب (بیش از حد میرایی) را تضمین کند، این رویکرد همچنین برای کلاس وسیع تری از مدل های فرآیند خطی در [22] دنبال شده است. اصلاحات بیشتر روش تنظیم از [22] شامل یک عبارت فیلتری اضافه شده به تابع انتقال کنترل کننده PID برای تسهیل تنظیم سرعت پاسخ حلقه بسته (زمان پاسخ) نسبتا ساده است [23]، و گسترش کنترل کننده PID با یک پیش مرجع مرجع. عمل فیلتر کردن یا وزن دهی برای تسهیل تنظیم سیستم حلقه بسته جداگانه با توجه به مرجع و اختلال خارجی [24]. با این حال، تنظیم خودکار کنترل کننده PID مبتنی بر اندازه بهینه فوق، راه ساده ای برای تنظیم میرایی حلقه بسته ارائه نمی دهد، در حالی که ادغام مکرر خروجی فرآیند ممکن است منجر به افزایش بار محاسباتی الگوریتم تنظیم خودکار کنترل کننده PID شود، به خصوص اگر کاربرد داشته باشد. بر روی یک کنترل کننده صنعتی نسبتا کم هزینه در نظر گرفته شده است. از این رو، یک روش تنظیم مانند قرار دادن قطب انعطافپذیرتر، و همچنین یک آزمایش تنظیم خودکار مبتنی بر پاسخ مرحله فرآیند سادهتر (به عنوان مثال بر اساس یک ادغام واحد پاسخ مرحله فرآیند) منجر به PID سازگارتر و کمتر میشود. تحقق تیونر خودکار برای این منظور، این مقاله یک رویکرد تنظیم کنترلکننده PID بر اساس معیار بهینه میرایی [34،35] در ترکیب با فرمولبندی مدل فرآیند PTn پیشنهاد میکند، که یک روش تحلیلی و ساده را برای تنظیم هر دو میرایی پاسخ حلقه بسته تسهیل میکند. سرعت پاسخ با توجه به پویایی فرآیند. تخمین پارامترهای مدل فرآیند PTn در اینجا بر اساس ادغام واحد پاسخ مرحله فرآیند به منظور یافتن پارامترهای مدل اصلی فرآیند FOPDT است. سپس مدل سادهتر FOPDT با استفاده از یک بسط تیلور مرتبه بالاتر از عبارت دینامیکی زمان مرده (تاخیر خالص) از طریق عبارات تحلیلی ساده، به مدل PTn بدون زمان مرگ معادل مرتبط میشود. تنظیم کنترلکننده PID پیشنهادی، روشهای شناسایی مدل فرآیند FOPDT و PTn و الگوریتم تنظیم خودکار کنترلکننده PID حاصل با استفاده از شبیهسازیهای کامپیوتری گسترده تأیید میشوند. مقاله بصورت زیر مرتب شده است. بخش 2 روش طراحی سیستم کنترل تحلیلی را بر اساس معیار بهینه میرایی و مدل فرآیند غیر تناوبی فشرده PTn ارائه میکند و اثربخشی بسته شدن حاصل را نشان میدهد.
تصویر برخی از نتایج
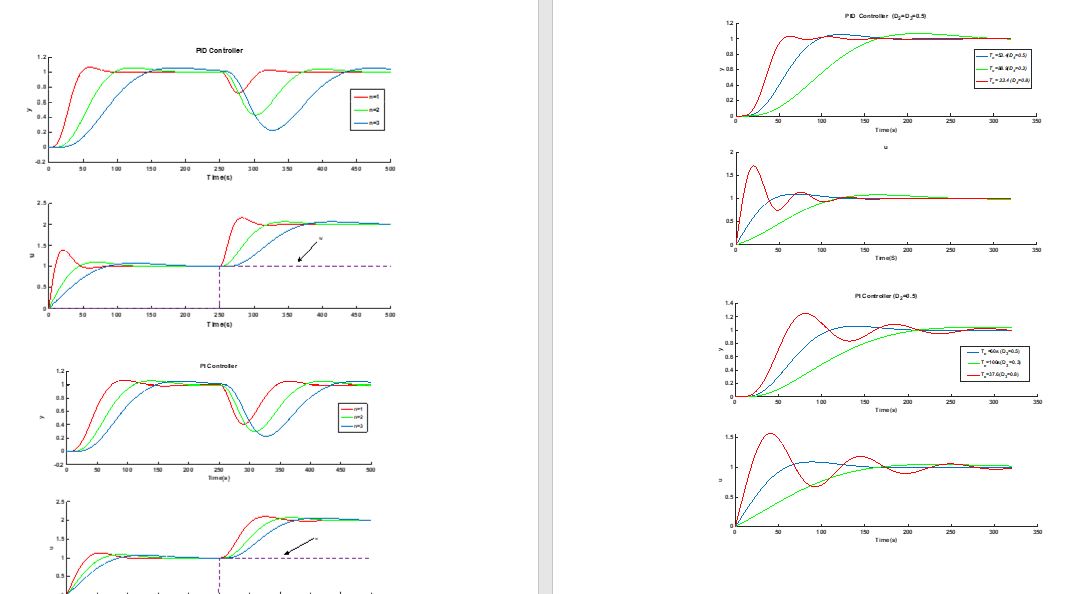
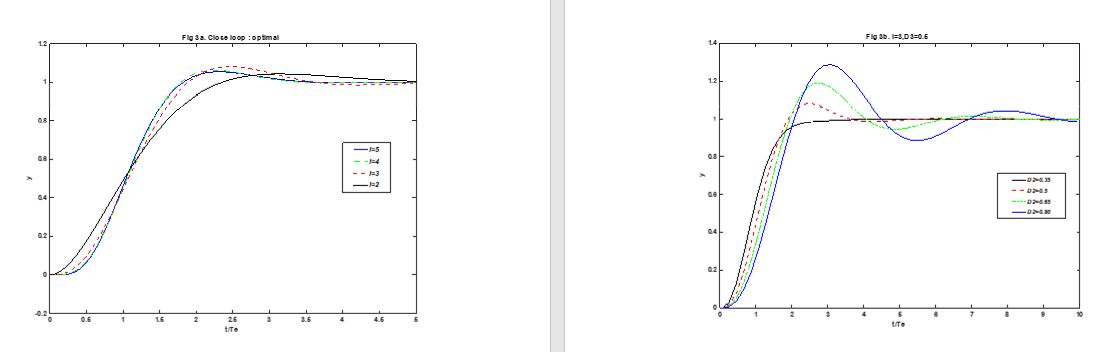
شبیه سازی آموزشی کنترل حالت لغزشی تطبیقی برای ردیابی مسیر ربات متحرک با متلب توسط کارشناسان گروه ۱.۲.۳ پروژه پیاده سازی گردیده است .
- فایلهای پروژه آموزشی به صورت کامل پس از خرید فایل بلافاصله در اختیار شما قرار خواهد گرفت.


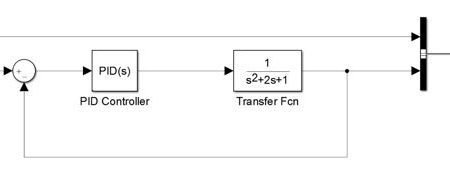

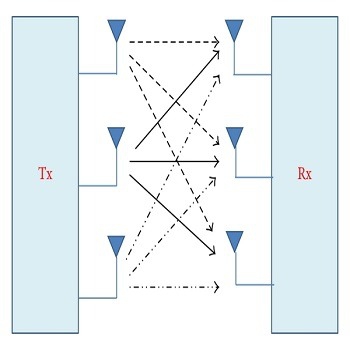
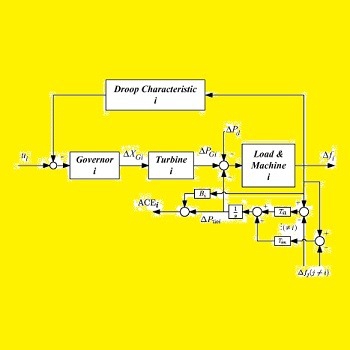






نقد و بررسیها
هنوز بررسیای ثبت نشده است.